In this task, we have a flag: mlnklfnknljflfjljnjijjmmjkmljnjhmhjgjnjjjmmkjjmijhmkjhjpmkmkmljkjijnjpmhmjjgjj
and the program with which it was encrypted. The program is similar to Caesar’s cipher, but:
- Size and alphabet: 16 characters (‘a’-‘p’) versus 26 (a-z).
- Intermediate encoding:
b16_encodeis used before shifting. - Shifted object: The result of
b16_encodeis shifted, not the original text.
Let’s look at the encryption program new_ceasar.py:
import string
LOWERCASE_OFFSET = ord("a")
ALPHABET = string.ascii_lowercase[:16]
def b16_encode(plain):
enc = ""
for c in plain:
binary = "{0:08b}".format(ord(c))
enc += ALPHABET[int(binary[:4], 2)]
enc += ALPHABET[int(binary[4:], 2)]
return enc
def shift(c, k):
t1 = ord(c) - LOWERCASE_OFFSET
t2 = ord(k) - LOWERCASE_OFFSET
return ALPHABET[(t1 + t2) % len(ALPHABET)]
flag = "picoCTF"
key = 'a'
assert all([k in ALPHABET for k in key])
assert len(key) == 1
b16 = b16_encode(flag)
enc = ""
for i, c in enumerate(b16):
enc += shift(c, key[i % len(key)])
print(enc)break down the code:
ALPHABET = string.ascii_lowercase[:16]: is a limited alphabet consisting only of the first 16 lowercase letters of the English alphabet.: 'abcdefghijklmnop'. Length ALPHABET = 16.
Method b16_encode(plain)
- Extracts
decimal asciivaluesc(for c in plain) adds zeros to make it 8 characters long and converts it to binary format. For example:ord('a')= 97 ⇒01100001 - divides into 2 parts:
[:4]- takes from the binary values digits by indexes from 0 to 3, than takes base 2 number and converts to decimal int num (it will be in range 0-15). Then throws it in search by index in ALPHABET and stores found letter from ALPHABET - same repeats for other part of binary value [4:] (indexes 4 - 7
Thus, method takes text from input, and outputs two other letters from the ALPHABET array for each letter taken by for loop.
Method shift(c, k):
- takes
сfrom string previously processed byb16_encode, and keyk, which may be 1 CHAR from ALPHABET. About it hints exception, that allkchars must be present in ALPHABET array and key length ==1
assert all([k in ALPHABET for k in key])
assert len(key) == 1- for
с,kfinds decimal ascii value and subtracts global variableLOWERCASE_OFFSET = ord("a")to make them all in range 0-15 (ALPHABET indexes): variablest1andt2 - Performs addition of these indices modulo the length of
ALPHABET(16). - The result is a new index, which is used to select a character from
ALPHABET.
That is, it is a classic affine cipher with addition, but with an alphabet length of 16 instead of 26.
- In the main body of the loop
for i, c in enumerate(b16), the methodenumerate(b16)returns a pair (index, value), and they are written each iteration ini, c. Therefore, will move tolen(b16) - 1. key[i % len(key)]- This expression determines which key symbol is used for shifting in a given iteration.i % len(key): Calculates the remainder of dividing the current indexiby the key length. Since the key length is 1,i % 1will always return 0 for any integeri. Probably, the author of the code just wanted to confuse people this way, because the key is always 1 character long and the modulus will always be 0.
In other words, to decrypt this algorithm, we need to create a program that will perform all actions in reverse order:
Here I described what it should perform:
unshift:
- takes encrypted
cchar andkkey - Finds their indexes (from their dec ASCII representations subtract LOWERCASE_OFFSET)
- recreate the original index (ciphertext character index - key index and then mod16 to make it in digits from 0 to 15)
ALPHABET[recreated index]
b16_decode:
- Takes a string whose characters are all present in ALPHABET
- Processes characters in pairs, since we converted the characters to binary code and divided them into
[:4][4:] - Finds the index in ALPHABET for each character, since in the original program we converted bits to dec and threw them into
ALPHABET[dec]. Now vice versa, the index ⇒ converts to a 4-bit representation. - Concatenates two numbers by 4 bits each back into an 8-bit string
- Converts this integer back to an ASCII character with
chr() - Combines all received characters back into a potential flag
All that remains is to write the final double loop, where the outer loop will iterate through the characters of ALPHABET in order to find the correct key, and the inner loop will take the key selected by the outer loop and take each ciphertext character mlnklfnknljflfjljnjijjmmjkmljnjhmhjgjnjjjmmkjjmijhmkjhjpmkmkmljkjijnjpmhmjjgjj and throw this pair into the unshift method, thereby extracting the b16 encoded string. Then the entire string will be passed to the b16_decode function, and so on for all possible keys (16 variants from ALPHABET):
NOTE
I duplicated code here: click
import string
LOWERCASE_OFFSET = ord("a")
ALPHABET = string.ascii_lowercase[:16]
ENCRYPTED_FLAG = "mlnklfnknljflfjljnjijjmmjkmljnjhmhjgjnjjjmmkjjmijhmkjhjpmkmkmljkjijnjpmhmjjgjj"
def unshift(c, k):
char_index = ord(c) - LOWERCASE_OFFSET # e.g for ord(b) - offset/ord(a) = 98 - 97 = 1
key_index = ord(k) - LOWERCASE_OFFSET # in this way we return the index of the character in the alphabet ALPHABET
return ALPHABET[(char_index - key_index) % len(ALPHABET)] # in the original cipher was ALPHABET[(t1 + t2) % len(ALPHABET)] that is, we added
def b16_decode(encoded_string):
decoded_chars = []
for i in range(0, len(encoded_string), 2): # iterate by 2
char1 = encoded_string[i]
char2 = encoded_string[i+1] #but for 1 iteration we will extract 2 characters, the i-th and the next one after it
val1 = ALPHABET.index(char1)
val2 = ALPHABET.index(char2)
binary1 = "{0:04b}".format(val1)
binary2 = "{0:04b}".format(val2)
eight_bit_binary = binary1 + binary2
dec_value_in_ascii = int(eight_bit_binary, 2)
decoded_char = chr(dec_value_in_ascii)
decoded_chars.append(decoded_char)
return "".join(decoded_chars)
print(f"Trying to decrypt for all {len(ALPHABET)} possible keys from ALPHABET: {ALPHABET}\n")
for key_char in ALPHABET: # we will search which of the 16 characters of ALPHABET will be VALID key, so this will be an outer loop
potential_b16_encoded = "" # first unshift to get the b16_encoded string, and then b16_decode it
for char in ENCRYPTED_FLAG:
potential_b16_encoded += unshift(char, key_char)
# for this key (we got string in base16) apply b16_decode
potential_flag = b16_decode(potential_b16_encoded)
if potential_flag != None:
print(f"Key: {key_char} -> Flag: {potential_flag}")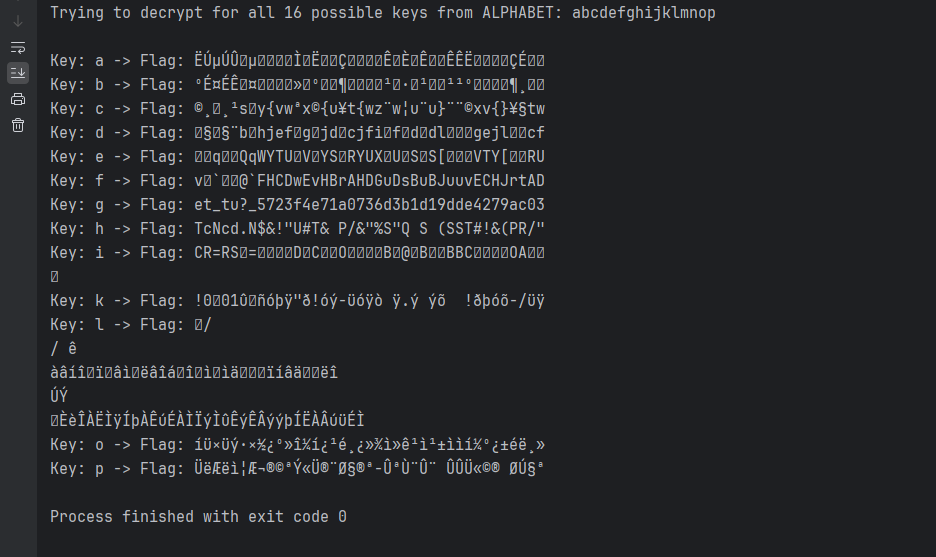
picoCTF{et_tu?_5723f4e71a0736d3b1d19dde4279ac03}