Mind your Ps and Qs

In this task, n and e are small. I search for “rsa small n and e attack” and find iroot method from gmpy2 module

RSA theory

RSA encryption uses the following parameters:

• n - module (product of two large prime numbers p and q)
• e - public exponent (usually 65537)
• d - private exponent (secret, required for decryption)
• m - message (plaintext)
• c - ciphertext

Encryption: c = m^e mod n
Decryption: m = c^d mod n

iroot

What does iroot do:

iroot(c, e) calculates the integer root of the e-th degree from the number c. Returns a tuple (result, is_accurate).

When working for RSA (Small e Attack):

This method works only when the message m is so small that:
m^e < n

In this case, during encryption, the module does not affect the result, i.e.:

c = m^e mod n = m^e (the modulus is not applied!)

Therefore, you can simply take the root of the e-th degree without knowing d:

m = iroot(c, e)[0] # we get the original message

Example when it works:

# If m = 100, e = 3, n = 100,000
c = 100^3 = 1000000
# But 1,000,000 mod 100,000 = 0 (the modulus is applied here)
 
# If m = 100, e = 3, n = 10000000 (large n)
c = 100^3 = 1000000
# 1000000 < 10000000, therefore c = 1000000 (no change)
# m = iroot(1000000, 3) = 100 ✓

So, I tried:

from gmpy2 import iroot
 
c = 8533139361076999596208540806559574687666062896040360148742851107661304651861689
n = 769457290801263793712740792519696786147248001937382943813345728685422050738403253
e = 65537
 
m = iroot(c, e)
print(m)

And got (mpz(1), False), which means that m^e >= N. So this method does not work.

factordb + python

Let’s try to factor n into prime factors p and q. n is small enough that this won’t take long.
n is small enough that it doesn’t take much time.

I used https://factordb.com:

and write a Python program to find d, calculate c^d mod n (decrypt), and convert the key and bytes:

TIP

This script as well as for other tasks I left here: click

from Crypto.Util.number import inverse, long_to_bytes
 
c = 8533139361076999596208540806559574687666062896040360148742851107661304651861689
n = 769457290801263793712740792519696786147248001937382943813345728685422050738403253
e = 65537
p = 1617549722683965197900599011412144490161
q = 475693130177488446807040098678772442581573
 
phi = (p - 1)*(q - 1)
 
# d = e^(-1) mod phi  | d is within the range from 1 to phi-1
# i.e., the inverse(e, phi) method finds the modular inverse of (e mod phi)
# that is, a number such that (e*d) mod phi == 1
# implements the "Extended Euclidean Algorithm"
d = inverse(e, phi)
 
m = pow(c,d,n) #c**d mod n
 
print(long_to_bytes(m))

As indicated in the code above, the inverse method from the Pycryptodome library implements the “Extended Euclidean Algorithm.” That is, it searches for the value d that:

• modular multiplicative inverse of the number e mod phi
• such a number exists ONLY if GCD(e, phi) == 1
• such a number d == e^(-1) mod phi(n)
• if you multiply d*e and then apply mod phi (d*e mod phi), the remainder MUST be 1

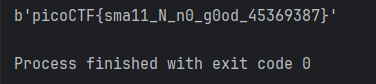
picoCTF{sma11_N_n0_g0od_45369387}